Contents | About | Contact

article 10, issue 03

Determination of Cycling Speed Using a Closed-form Solution from Nonlinear Dynamic Equations

Junghsen Lieh
December 21, 2006

 

Abstract

The theme of this paper is to develop a closed-form method to solve nonlinear equations for cycling speed. The nonlinear equations are derived from force and power balance. The closed-form solution for the force equation is straightforward, yet the closed-form solution for the power equation is obtained by means of a partitioning technique. Finally a simulation is used to study the effect of the air drag coefficient, frontal area, rolling resistance, road gradient, and power consumption.

[Editor's note: The following presentation is a shortened version of the full paper in PDF format [200 kB].   It is an advancement on HPeJ Article 1, where similar equations are presented but without their derivations. In contrast to numerically calculated solutions for developing a time history, Junghsen Lieh's steady-state and dynamic-state equations produce results whose accuracy is not limited by time-step increment size. Also, computers or other programable devices are not required; an ordinary scientific calculator (or slide rule) is sufficient to obtain solutions.]

Introduction

A number of researchers have investigated the effect of aerodynamics on cycling speed, however there is lack of a general closed-form solution for cycling speed and the estimation of vehicle speed was normally done numerically in a tedious and time-consuming spreadsheet or in a commercial program.

This article presents a closed-form method. The nonlinear equations for cycling are formulated and expressed in terms of velocity and key vehicle parameters.

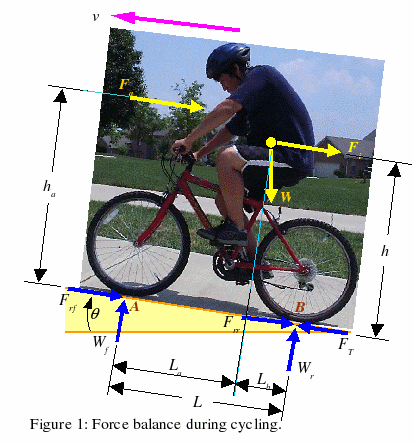
Traction and Resistant Forces

As shown in Figure 1, the major external forces to be overcome by the tire traction force (F_T) during cycling are

F_a aerodynamic force
F_r rolling resistance
F_i inertia force  [the wheels' rotational inertia is neglected, Ed.]
F_g gravitational force

The dynamic equilibrium of the system along the longitudinal direction can be written as

F_T = F_a + F_r + F_i + F_g

Using weight values W = W_f+ W_r= mg and summing the moments about point A (without considering the airlift effect), the normal load on the driving wheel is

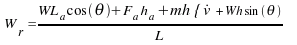
Define μ_p as the peak coefficient of tire-road friction and N = W_r as the normal load on the driving wheel. For the current study,it is assumed that the traction force is near its peak value such that the maximum theoretical speed may be obtained, i.e.

F_T = μ_p N

Define m as the mass of bicycle plus the rider, ρ as the air density, Cd as the air drag coefficient, A_f as the frontal area, v the forward velocity, Θ as the grade angle, g as the gravitational acceleration, and f₀ and f₁ as the rolling resistance coefficients (f₁ is usually very small but is included here for completeness). The air drag, rolling resistance, inertia and gravitational forces can be expressed in the following form:

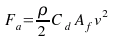
F_r = (f_o + f₁ v²) W  

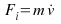
F_g = W sin(Θ)

Where,.   Substituting these forces into the first equation, a nonlinear equation describing the dynamic equilibrium can be written in the following form:

  [Eqn A]

Where, the expressions for s_i are

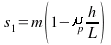
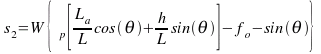
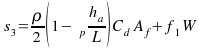
[Eqn A] represents the tire traction capability of a bicycle when its power availability is adequate or unlimited. Since the bicycle is a rear-wheel drive system, the rear normal load is used to determine the traction force, i.e. N = W_r.  The theoretical maximum speed is found by setting , as a result, [Eqn A] is reduced to

s₂ - s₃v² = 0

The maximum speed based on tire traction capability is

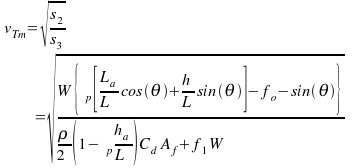
To find the time history of velocity, requires an integration of [Eqn A].  [for derivation see full paper, Ed.]

If the bicycle starts from rest,the velocity can be expressed as:

  [Editors' note]

Power Equation

The above closed-form solution for maximum speed represents the maximum tire traction condition, which for a bicycle or human-powered vehicle is generally only met in slippery conditions because of the human's limited strength. In the following the rider’s power output is now considered. [for derivations and full results see full paper, Ed.]

Define P_T the rider’s total available power. The power transmitted to the rear wheel is modified by the cycling efficiency η

P_w = ηP_T = (F_a + F_r + F_i + F_g)v

Define the constants:

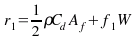
r₂ = W [ƒ_o + sin(>Θ)]

r₃ = ηP_T

When the bicycle starts from rest, i.e. v = 0, the equation is singular. This implies that the acceleration can be high when the speed is near zero.

The maximum speed is obtained by setting = 0.   This leads to

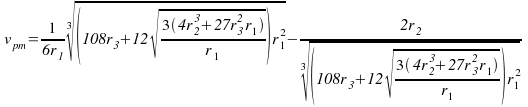
The maximum speed based on a given power output v_pm is the real root of this, i.e.

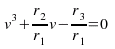
Summary

Based on the nonlinear equations derived from force and power equilibrium, closed-form solutions for determining cycling speeds are obtained. With the closed-form solutions, the estimation of maximum speeds becomes straightforward and the evaluation of vehicle performance under the influence of vehicle parameters (such as air drag, frontal area, power, mass, and rolling resistance) becomes simple and easy.

Simulation Results

Simulation graphs are shown for variations of air drag coefficient, frontal area, rolling resistance coefficient, mass, and road gradient. 

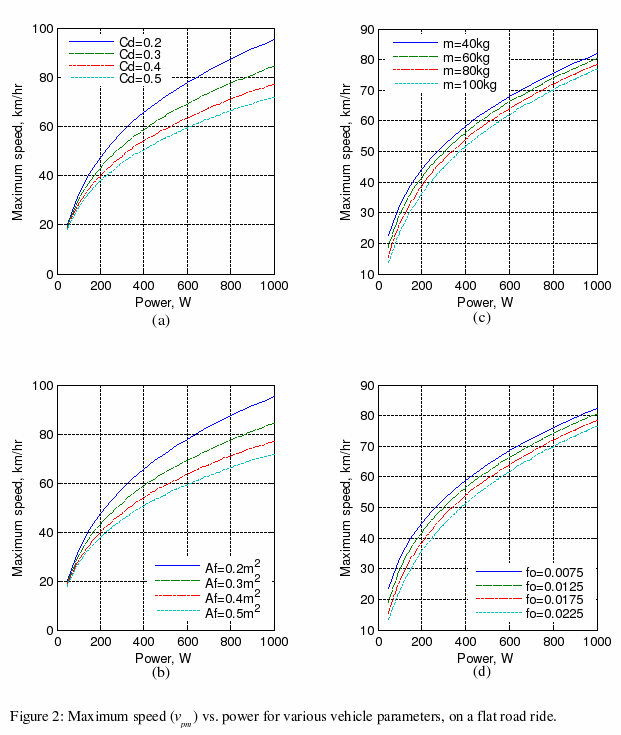
In Figure 2, Part (a) is for the effect of air drag coefficient C_d, Part (b) for the effect of frontal area A_f, Part (c) for the effect of mass m, and Part (d) for the effect of rolling resistance coefficient f_o.

In Figure 3, if the air drag coefficient, frontal area, and rolling resistance coefficient are low as in Part (d), a 60-kg racercan reach 90 km/h on a flat road and 30 km/h on a 9 %-uphill gradient with [given sufficient duration] 500 W power. For the higher resistance values in Part(a), the maximum speed is 58 km/h on a flat road and 18 km/h on a 9 % uphill-gradient.

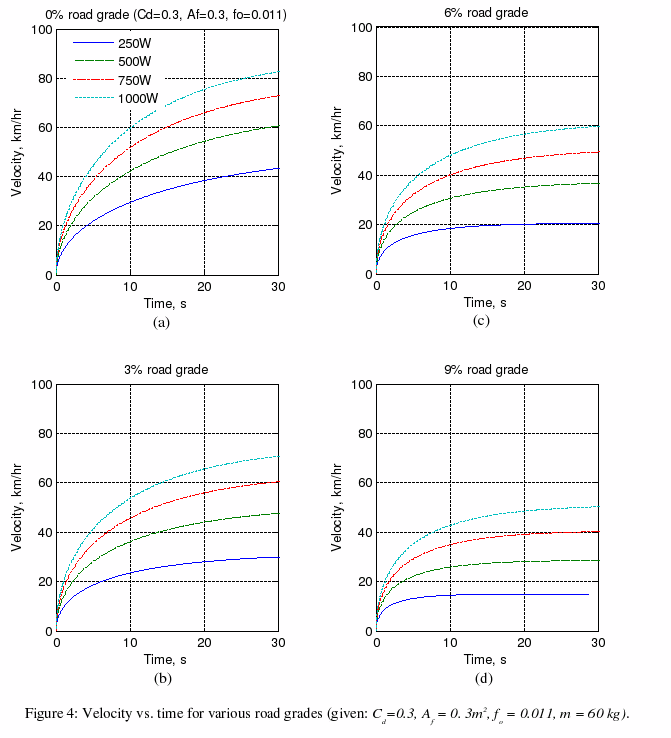
In Figure 4, it can be seen that the velocity reaches 42 km/h in 30seconds if the rider delivers 250 W on a flat road, or 60 km/h for 500 W. For a 9 % uphill-gradient the values are 15 km/h for 250 W or 28 km/h for 500 W.

Files for calculation:

The above graphs can be generated using Matlab and this file provided by the author, or Scilab and this file. Scilab is a free open source platform for numerical computation which can also import and convert Matlab files. After installing Scilab, download the file, open it in Scilab's editor, change any values you want, and execute it.
Also provided a spreadsheet: velomobile-speed-2methods.ods [Ed.]

References:

see full paper

About the author:

Junghsen Lieh, PhD
is Associate Professor for Mechanical & Materials Engineering
at Wright State University, Dayton Ohio 45435 USA

He is the adviser for the university's ASME HPV student group and has been involved with solar racing. His extensive research interests include intelligent control systems, multibody nonlinear dynamics, vehicle engineering, biomechanics, finite element analysis, and metal forming.

Contact:
(937) 775-5040 (ph); (937) 775-5009 (fax)
jlieh AT cs.wright.edu 

Homepage:
http://www.cs.wright.edu/~jlieh/jlieh.html

Contents | About | Contact

Human Power eJournal